Fibonacci: Nature’s Mathematics

It’s as easy as 0, 1, 1, 2, 3

By Gordon A Maclean, PhD

Well, if I haven't lost you already, that's a good start. Simply hearing or reading the word "math" can send people running. And besides, what does math have to do with nature, except when laying out your garden spacing or flowers. Right? Wrong!

Nature is full of math. It's built into the entire ecosystem and one of the greatest math discoveries of all time is the relationship between the Fibonacci Sequence and some basic constructs of nature. Knowledge of the sequence goes back to Sanskrit writings of the 13th century BCE but is generally credited in Western mathematics to Leonardo Bonacci of Pisa (aka "Fibonacci") in 1202 CE.

The Fibonacci Sequence starts with the values of 0 and 1. You add those together and from there on you add the previous two numbers in the sequence. With that simple rule, you have the series of values 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, and so on.

An amazingly simple process, yet this set of values appears more than one would think throughout nature. The easiest place to find this sequence is in flower petals. Most have three petals (lilies, irises, trilliums), five petals (parnassia), eight petals (Black-eyed Suzie's), or 13 (many daisies).

Trillium (three petals)

 Marsh Marigold (5 petals)

 Black-eyed Suzie's (8 petals)

There are other sequences, similar to Fibonacci’s that cover other common objects that have arrangements of four or seven. But these tend to be much less common. Think of how rare it is to find a four-leafed clover.

The Fibonacci Sequence also describes many leaf arrangements, especially where spirals are involved. The classic example is the leaf arrangements on trees. Starting with any leaf on a stem, you will find that there will eventually be a leaf in that same stem position. The number of times the leaves spiral around the stem and the number of leaves in the sequence are usually Fibonacci Sequence numbers.

Look at the following diagram. The arrangement of leaves on a branch follows a very specific pattern within a species. In the case of the elm tree, starting at any leaf, there will be another leaf in the same position two leaves later, in just one spiral around the branch. It takes five leaves and two spirals to come back to the same point in the pattern on cherry trees. For pear trees, its eight leaves along five spirals. Honestly, sometimes these can be hard to see, especially when leaves get knocked off of branches by wind, critters, or other disruptions, but they are real.

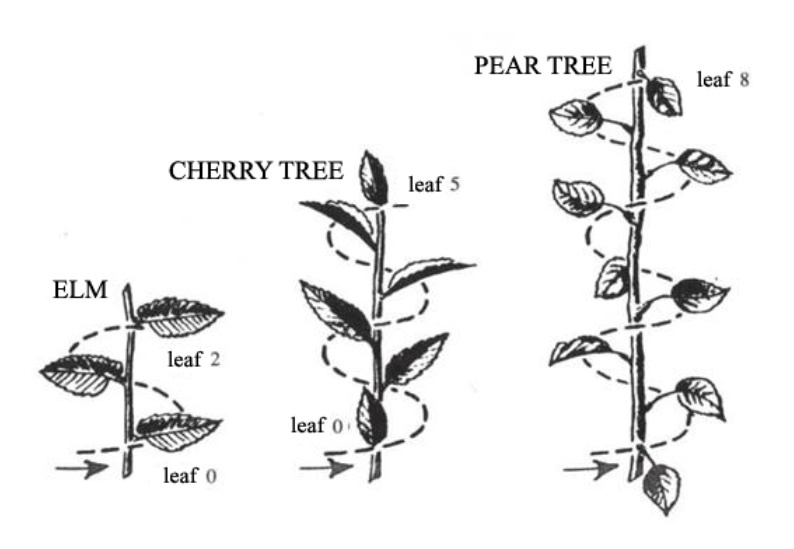
From: https://surajeselsohn.com/2021/05/04/fibonacci-numbers-are-plants-mathematicians/

A pineapple is full of Fibonacci and it doesn't detract from the taste. The technical term for this is "parastichy," which is defined as "secondary spirals winding in opposite directions in certain botanical structures" and sometimes called a "double helix."

On the face of the pineapple, there are five-sided scales arranged in a double helix, each spiral of scales counts to a Fibonacci number, depending on whether you count clockwise (13 scales top to bottom) or counter-clockwise (21 scales).

Pinecone scales are a bit different. They frequently have eight right-handed spirals when looking from the top of the cone and 13 left-handed spirals. There are other spirals in the arrangement when you look at them more "vertically." It is difficult to do, but the number always ends up being a Fibonacci number. See http://faculty.smcm.edu/sgoldstine/pinecones.html for more information.

Sunflower floret arrangements (21 and 34) are other classic examples of Fibonacci showing in nature. About 80% of sunflowers follow this pattern. Most of the remaining 20% closely approximate the Fibonacci numbers.

Why does nature keep reverting to this mathematical sequence? There are a couple of reasons. First, for the leaf arrangement example above following a Fibonacci sequence greatly reduces the chance for self-shading. If you are a tree and you are using your energy to put out leaves to collect sunlight to create more energy for yourself, the last thing you would want is your leaves shading each other. You get enough competition from the other trees around you; best not compete against yourself.

In the case of pineapple, pinecones, and sunflowers, the reason is that these spirals present an elegant solution to a very difficult problem. Pineapples, when newly formed, have the same number of scales as one that is fully formed. Same with pinecone scales and sunflower seeds. They start with a complete set and their numbers don't increase. But the size of each individual does increase.

A newly formed pinecone has many scales as a fully formed pinecone. The problem then is how does the pinecone (or pineapple) grow? Its scales get bigger. And the only way for all the scales to get bigger and not form gaps or crowd out their neighbors is to arrange the scales in spirals, and those spirals work best when they form in Fibonacci sequences.
Many desert succulents follow Fibonacci patterns. Can you count the spirals? The right-hand spiral is pretty obvious; you have to look harder for the left-hand spiral.

Maybe the most dramatic example of Fibonacci sequences in nature occurs when we turn the numbers themselves into a graphical spiral. If you start laying out those values as the dimensions of a set of squares and arrange them properly, then draw a quarter circle in each square; the result is called a Fibonacci Spiral.

The typical textbook example of a Fibonacci Spiral has it overlain on a Nautilus Shell.

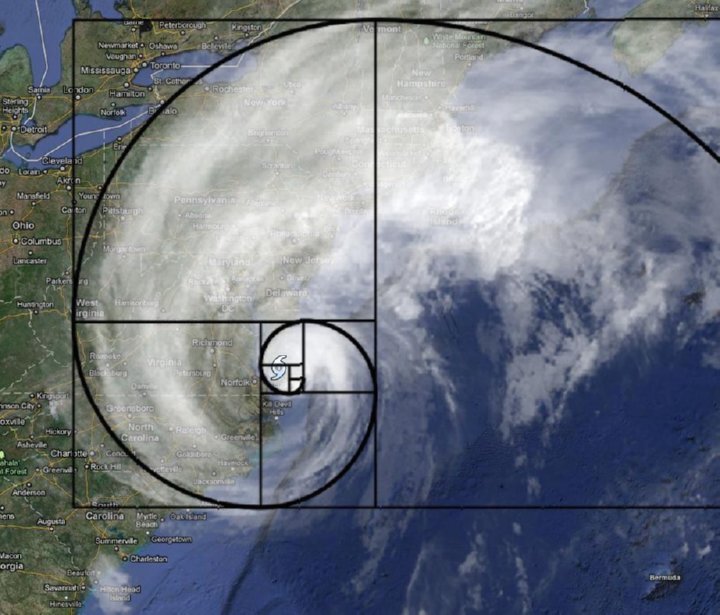
The next few examples show how dynamic energy systems take on significant aspects of the Fibonacci spiral. Computer modeling has shown that these spirals represent energy organization with limited energy losses in these cases. In other words, the system is energy-optimized.

Sometimes we only see a portion of the sequence, but the remainder is hidden out of sight—for example, a breaking wave (From https://innersense-inc.com/wp-content/uploads/2020/09/Golden-Ratio-Ocean-Wave-1200x796.png).

A spiral galaxy with two Fibonacci Spirals overlain (From https://blogs.glowscotland.org.uk/glowblogs/cbteportfolio/2017/11/24/maths-in-art-and-the-fibonacci-sequence/).

Hurricane Irene
https://insteading.com/assets/images/Art/Fibronacci/hurricane%20spiral.jpg

And with all of these spirals, it's really not hard to find them on your own once you know what to look for.

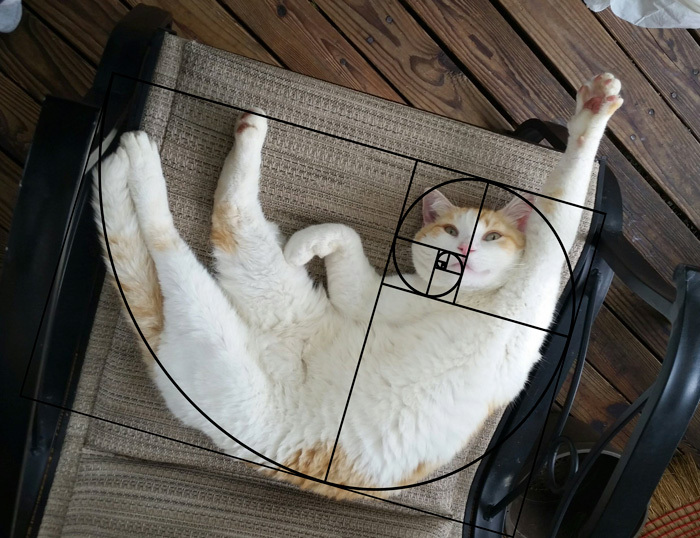
Take a look around. You may need to look no further than your fur baby. If she's in the right mood, she might just display some Furbinacci!

Fibonacci’s sequence is a beautiful, and elegant, mathematical way to describe many features found in nature. Once you start looking for them, and knowing what it is, you will find a greater insight to the structure of the world around us.

(See more fascinating images of designs in nature on our Video page.)